
関連するソリューション

業務改革

AI
フェロー 玉越 元啓

はじめに:「Neurosymbolic AI」— 学習×推論で“説明できるAI”へ
2025年は生成AIが席巻した年となりましたが、2026年に企業の現場で問われるのは、高精度でありながら根拠を示し、規制や社内規範と整合できるAIだと考えています。ニューラルネットの学習能力と、論理・ルール・知識グラフによる推論を同一システムで統合し、説明可能性・整合性・安全制約を実務レベルで両立させるNeurosymbolic AI(ニューラル+シンボリックAI)を紹介します。
定義や表記(neurosymbolic/neural‑symbolic/neuro‑symbolic)は複数併存しますが、近年の総説では同義として扱われるのが一般的です(後述します)。

Neurosymbolic AI とは何か
背景
シンボリックAIは、明示的な知識表現(ルール、論理式、知識グラフ)と推論エンジンを中核として、人が読める形で根拠や手続きを追跡できるのが強みです。とりわけ知識表現と推論(KR&R)の文脈では、一階述語論理や制約、推論規則などを用いることで、規制遵守や監査に耐える説明性を提供できます。一方で、大規模で曖昧なデータを直接扱う柔軟な学習は不得手です。
対してニューラル(接続主義)は、大量の非構造化データから表現学習・汎化に優れるものの、根拠の可読性・常識的整合・ハードな制約順守は苦手です。
Neurosymbolicは、両者の補完関係(学習の強み+推論の強み)を同一ワークフローで統合し、高精度×説明性×規範整合を同時に満たすことを狙います。こうした統合は、近年の総説・レビューでも「次の波(3rd Wave)」として整理されています。
まさに今、“高精度×説明性×規範整合”を現場で実装可能な形でもたらし始めています。
Neurosymbolic AIの歴史
シンボリックAIとニューラルネットワークを統合するというアイデアは1980年代にまでさかのぼります。Smolensky による Integrated Connectionist/Symbolic (ICS) の構想(1988)が、接続主義と記号主義の統合という理論骨格を提示しました。[R1]
“Neurosymbolic”という語の学術的使用は1995年の ESANN(Hilario ら)で確認され[R3/R4]、2002年には Garcez・Broda・Gabbay によるモノグラフが“neural‑symbolic”の名称で分野を体系化しています。2016年以降の Logic Tensor Networks (LTN)などは、微分可能な一階論理×NNを打ち出し、学習と推論の同時最適化が現実味を帯びました。[R7]
2020年代は「第3の波」として再定義され、用語の表記ゆれ(neural‑symbolic/neurosymbolic)も包括的に整理されています。[R8]
年表(筆者まとめ)
- 1988:Smolensky「On the Proper Treatment of Connectionism」— ICS構想の土台。
- 1990–1993:Shastri & Ajjanagadde(SHRUTI)— 同期発火で動的束縛とルールを神経回路網へ。
- 1995:Hilario ら「Neurosymbolic integration: unified vs. hybrid」(ESANN)— neurosymbolic語の最古級使用。
- 1996–1997:Hilario「An Overview of Strategies for Neurosymbolic Integration」 [R11]
- 2002:Garcez, Broda, Gabbay『Neural‑Symbolic Learning Systems』— 分野を体系化。[R12]
- 2006:Richardson & Domingos「Markov Logic Networks」— 論理×確率の橋渡し。[R13]
- 2016–:Serafini & d’Avila Garcez「Logic Tensor Networks」— 微分可能論理×NN。 [R14]
- 2020/2023:d’Avila Garcez & Lamb「The 3rd Wave」— 近年の再定義。 [R15]
- 2022:Hitzler ら(NSR)— 定義・動向の包括的整理、表記の包括的扱い。[R16]
事例
事実、2025年には、Neurosymbolicの実装事例が加速しました。GartnerのAIハイプサイクルでは、知識グラフ基盤(例:AllegroGraph[1])がNeurosymbolicの企業適用を支える技術として注目され、規制産業(医療・金融・法務など)での説明可能性ニーズが追い風となっています。また、Amazonによる倉庫ロボ/ショッピング支援への採用報告、欧米を中心としたスタートアップの台頭(ExtensityAI、Permion ほか)[3]も相次ぎ、産業適用の射程が広がっています。- [The Rise of Neuro‑Symbolic AI: A Spotlight in Gartner’s 2025 AI Hype Cycle] https://allegrograph.com/the-rise-of-neuro-symbolic-ai-a-spotlight-in-gartners-2025-ai-hype-cycle/
- https://neurosymbolic-ai-journal.com/system/files/nai-paper-843.pdf
- https://www.startus-insights.com/innovators-guide/neurosymbolic-ai-companies/

Neurosymbolic AI のアルゴリズム
基本構造:表現層×推論層×制御層
Neurosymbolicの“型”は複数ありますが、基本的に、表現層 × 推論層 × 制御層で構成されます。図1. Neurosymbolic AIの基本構造
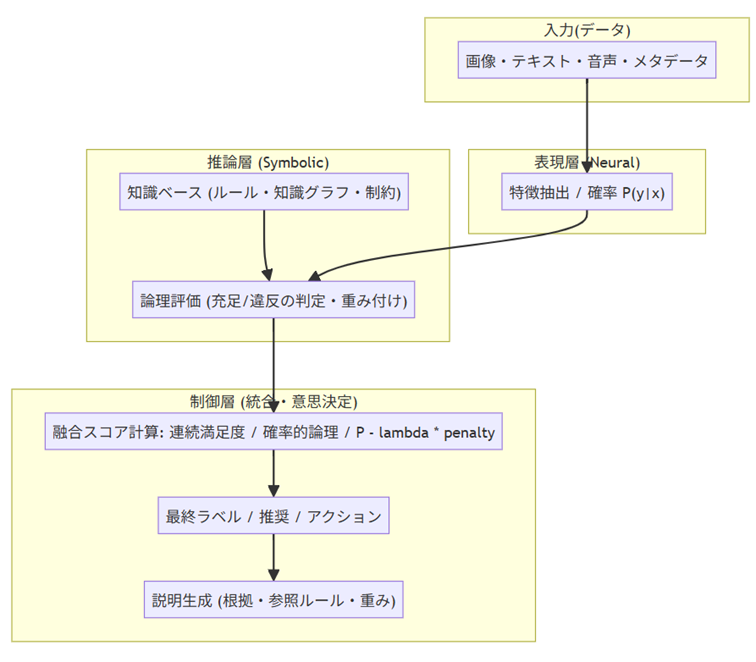
- 表現層(Neural):画像・文章などからモデルが確率や特徴を出します。ニューラルネットワークやディープラーニング等でパターン認識を行い、分類確率や埋め込み(特徴)を出します。
- 推論層(Symbolic):ルール・知識グラフ・制約で一貫性チェックや推論など“してよい/よくない”を照合します。
- 制御層(統合):両者をひとつの基準(スコア)にまとめ、最終判断と説明を出します。実装の違い(LTN/MLN/ペナルティ加算)に関わらず、「確率×ルール」を1つにまとめて説明や根拠を残すことが共通点です。
一般的なアルゴリズム
一般的なNeurosymbolic AIのアルゴリズムは、以下の流れとなります。- 入力を用意する(例:画像・文章・ログ)。AIが読み取れる形にして渡します。
- 表現層がパターンを読み取り、分類確率や特徴を出します(「それらしい度合い」を数値化)。
- 推論層がルール・知識に照らしてチェックします(してよい/よくない、矛盾の有無)。
- 制御層が両者を1つのスコアに統合して結論を出します(確率が高くても重大な違反なら減点)。
- 説明を表示・保存します(どのルールが何点効いたか=根拠をログ化)。
表現層と推論層の統合パターン
- Neuro→Symbolic
ニューラルでパターンを捉え、記号(述語・関係)に写像して論理推論へ渡すスタイルです(例:連続値の論理満足度を最大化するLTN系)。
- Symbolic→Neuro
ルール・制約で学習を誘導(制約を損失に組み込む、弱教師に使う等)し、学習を“安全・高信頼”方向へガイドするスタイルです。
- 双方向ハイブリッド
両者が相互作用し、学習と推論を共同最適化するスタイルです(例:確率的論理で知識の重みを学習しつつ推論、連続論理で端から端まで微分可能に最適化)。
シンボリックで論理推論する主要な方法
どれも“知識をルールやグラフで明示し、判定の根拠が追える”のが共通点です。使い分けの“勘どころ”だけ押さえてください。- ルールベース(一階述語論理/規則エンジン)
IF–THEN規則や述語(例:isBird(x) ⇒ hasWings(x))で明確な業務ルールを表します。監査・規制に強みを発揮します。
- オントロジー+知識グラフ推論(RDFS/OWL/SHACL等)
用語の定義・階層関係・整合性を管理し、型違反や必須関係の欠落を検出します。企業内語彙の統一に効果的です。
- 制約ベース推論(制約充足・最適化)
“必ず満たすべき”ハード制約や“できれば満たしたい”ソフト制約の満足度で判断します。組合せ条件や安全基準の適合に向いています。
- 確率的論理(Markov Logic Networks など)
論理式に重みをつけ、「満たすほど尤度が上がる」モデル。不確実性を含むルールを確率的に運用できます。
- 微分可能論理(Logic Tensor Networks など)
論理の真偽を0〜1の連続値で扱い、学習と推論を一体化します。ディープラーニングと同じ学習基盤で“ルールの満足度”を最適化できます。

実践
Neurosymbolic推論の流れ(統合スコアと説明)
本稿のデモでは、ニューラル部の確率 P(y|x) と、ルール違反のペナルティ(λ・penalty) を統合し、score = P(y|x) − λ・penalty(y, x) を最大化するラベルを選択しています。出力では 「違反ルール一覧」 を同時に提示し、意思決定の根拠を明示します。こうした可観測な論理は、規制産業・安全領域における“説明できるAI”の基盤になります。
1.二重ものさし(確率×ルール)、2.即時の説明出力、3.λで政策調整、4.知識の独立管理—この4点が、本デモにおけるNeurosymbolicらしさです。精度だけではない“根拠と運用”を重視する現場に適した構造になっています。これらについて下で解説します。
コードのポイント解説
1.確率×ルールの “二重ものさし” で決める(Neural→Symbolic 融合)score = probs[idx] - lambda_penalty * pen本デモの最重要ポイントは、ニューラルの確率 P_nn と ルール違反の重さ(penalty) を 1つのスコアにまとめて意思決定していることです。
score = P_nn - lambda * penalty という形で融合しており、高い確率でも重大な違反があれば却下方向に傾きます(neuro_symbolic_predict() 内の計算)。安全や規制を重視する現場に向いた設計です。
2.説明(根拠)を“その場で”出せるログ構造
evidence[lab] = {"p_nn": probs[idx], "penalty": pen, "score": score, "violations": vio}予測時に、各ラベル候補について p_nn(確率)/penalty(違反合計)/score(統合スコア) を出し、違反ルールの一覧を併記します(evidence 構築と print 出力)。「何が理由で下げられたか」を 1行で理解でき、監査やレビューに即使える形です(ログ例:- ルール違反: ...)。
3.ポリシーの強弱を運用ダイヤル(lambda_penalty)で調整
def neuro_symbolic_predict(x, lambda_penalty=1.0, verbose=True):ルールの強さは引数 lambda_penalty で即時に調整できます(例:λを上げる=規範優先、下げる=確率優先)。モデルを触らずポリシーだけ切り替えられるのは、Neurosymbolicの運用しやすさをよく表しています。将来的に クラス別λ や ハード制約(違反なら即棄却) に拡張すれば、細かな現場要件にも対応しやすくなります。
4.“知識層”をモデルから分離:学び直さずに“ふるまい”を変えられる
rules = [
Rule("dog", lambda f: (f["legs"] == 4) and (not f["has_wings"]) and (not f["habitat_water"]),
penalty=0.40, description="dogなら4脚・翼なし・水生でないはず"),
Rule("dog", lambda f: f["bark"] and (not f["meow"]),
penalty=0.25, description="dogなら吠える傾向・猫鳴きでない"),ルール定義(rules)が独立しており、人が読める説明文も付与されています。再学習(retrain) なしで知識だけ差し替えられるため、制度改定や運用判断の変更に迅速に追随可能です。Neural(学習)とSymbolic(知識)を分けて持つ、この二層設計こそが Neurosymbolic の本質です。
実行ログと解説
凡例- P_nn:ニューラル部の確率 P(y|x)
- penalty:ルール違反の合計ペナルティ
- score:最終スコア(デモでは score = P_nn - lambda * penalty、lambda=1.0)
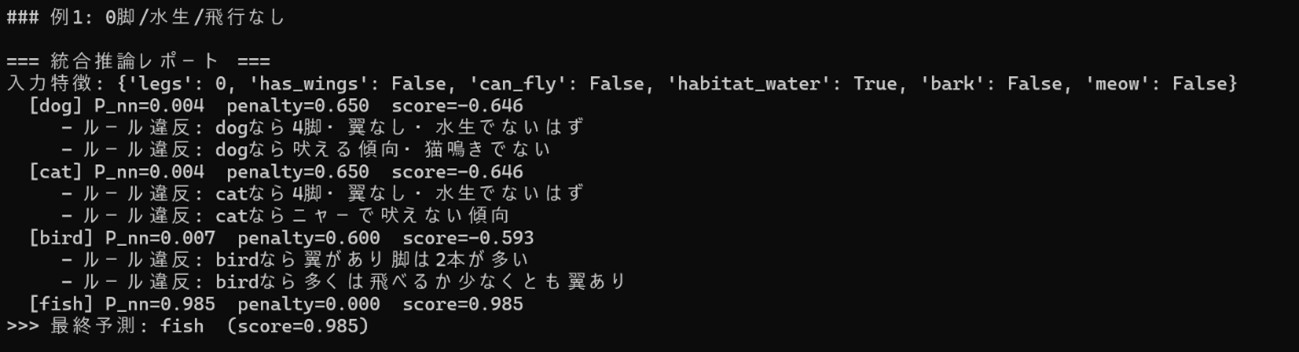
fish はルール違反がゼロで、ニューラル確率も0.985と非常に高く、満点に近いスコアで採択されています。モデル確率とドメイン知識が一致した理想ケースで、説明(違反なし)も明快です。
例2:4脚/吠える/水生=1(dogっぽいが水生)
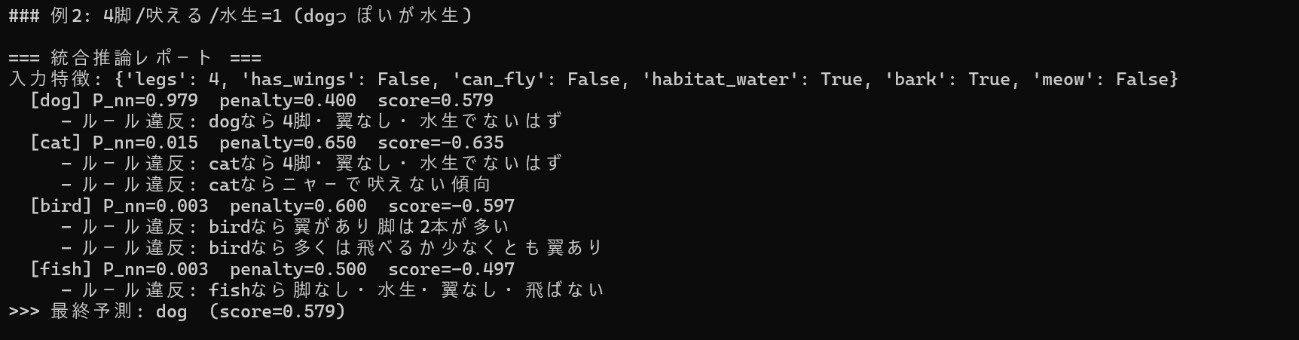
水生=1がdogのルールに反するため、dog に0.400の減点が入ります。それでもニューラル確率が非常に高く、総合スコアでは dog が勝つ結果に。確率とルール違反のせめぎ合い(トレードオフ)が見える例です。より厳格にする場合は、lambdaを上げるか、「水生のdogは禁止」というハード制約にすると、dog は採択されなくなります。
例3:4脚/ニャー=1/吠える=1(dog と cat が同点)
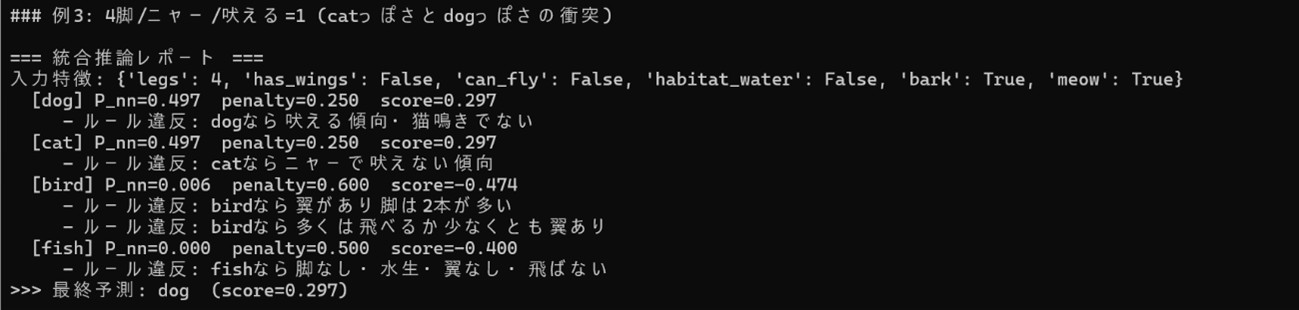
dog と cat が確率・違反ともに同値で、scoreが同点になっています。本デモの実装では評価順の都合で dog が選ばれています。
実務では、
- タイブレーク規則(例:違反数の少ない方/重要度の高いルールを優先)を明示
- クラス別lambda(ルールの重み)で業務優先度を反映
- 必要に応じてハード制約(即棄却)を導入
まとめ
以上の例から分かるように、Neurosymbolicではモデルの確率とルールの整合性をひとつの指標に統合し、違反ルール一覧という根拠とともに最終判断を提示できます。これにより、“精度が高いのに危ない判断”を未然に抑止しつつ、説明できる意思決定が可能になります。
全体をとおして
2026年は、Neurosymbolicのスケーラビリティ/メタ認知が鍵になります。大規模知識の取り込みや、モデル自身が推論の信頼度を自己評価する仕組みが成熟すれば、現場適用の幅はさらに広がります。SIerは、業務ルールの整備と、その品質保証(整合性・矛盾・カバレッジ)を継続できる体制を整え、説明ログの標準化を推進しましょう。年初の今、生成AIを超えた「学習と推論の融合」に投資する意義は大きいはずです。「最初はルールを少なく、重要なハード制約から」:安全・規制に直結する条件だけを先に入れるのが王道。違反は即NGにしておくと、精度が高いのに危ない判断を未然に防げます。
「説明ログを習慣化」:結果と一緒に根拠(どのルールが何点効いたか)を保存。監査・再発防止・改善会議で再利用できる資産になります。
「統合の強さ(λや重み)は“運用基準”とセットで」:クラス別λや重みは、誰が・いつ・なぜ変えたかを台帳管理。ハード制約は変更に承認フローを。
付録
サンプルコード
体験できるサンプルコードです。出力結果や表示内容は紙面解説等の都合によりコードの一部は記事とは異なっています。# -*- coding: utf-8 -*-
import numpy as np
np.random.seed(42)
labels = ["dog", "cat", "bird", "fish"]
def make_sample(legs, has_wings, can_fly, habitat_water, bark, meow, y):
return np.array([legs, has_wings, can_fly, habitat_water, bark, meow], dtype=float), int(y)
# ---------- 合成データ ----------
features_list = []
labels_list = []
for legs, has_wings, can_fly, habitat_water, bark, meow, y in [
(4,0,0,0,1,0,0),
(4,0,0,0,1,0,0),
(4,0,0,0,0,1,1),
(4,0,0,0,0,1,1),
(2,1,1,0,0,0,2),
(2,1,1,0,0,0,2),
(0,0,0,1,0,0,3),
(0,0,0,1,0,0,3),
]:
x, label = make_sample(legs, has_wings, can_fly, habitat_water, bark, meow, y)
features_list.append(x)
labels_list.append(label)
X_train = np.array(features_list, dtype=float)
y_train = np.array(labels_list, dtype=int)
# ---------- ニューラル部 ----------
n_features = X_train.shape[1]
n_classes = len(labels)
W = np.random.randn(n_features, n_classes) * 0.01
b = np.zeros((1, n_classes))
def softmax(z):
z = z - z.max(axis=1, keepdims=True)
exp = np.exp(z)
return exp / exp.sum(axis=1, keepdims=True)
def forward(X):
z = X.dot(W) + b
return softmax(z)
def one_hot(y, n):
y = y.astype(int)
oh = np.zeros((y.size, n))
oh[np.arange(y.size), y] = 1
return oh
def train(X, y, lr=0.1, epochs=500):
global W, b
Y = one_hot(y, n_classes)
for e in range(epochs):
P = forward(X)
loss = -np.mean(np.sum(Y*np.log(P+1e-12), axis=1))
grad = (P - Y) / X.shape[0]
dW = X.T.dot(grad)
db = np.sum(grad, axis=0, keepdims=True)
W -= lr * dW
b -= lr * db
if e % 100 == 0:
print(f"[epoch {e}] loss={loss:.4f}")
train(X_train, y_train, lr=0.2, epochs=600)
# ---------- シンボリック部 ----------
class Rule:
def __init__(self, target_label, condition_fn, penalty, description):
self.target_label = target_label
self.condition_fn = condition_fn
self.penalty = float(penalty)
self.description = description
def feature_dict(x):
return {
"legs": int(x[0]),
"has_wings": bool(int(x[1])),
"can_fly": bool(int(x[2])),
"habitat_water": bool(int(x[3])),
"bark": bool(int(x[4])),
"meow": bool(int(x[5])),
}
rules = [
Rule("dog", lambda f: (f["legs"] == 4) and (not f["has_wings"]) and (not f["habitat_water"]),
penalty=0.40, description="dogなら4脚・翼なし・水生でないはず"),
Rule("dog", lambda f: f["bark"] and (not f["meow"]),
penalty=0.25, description="dogなら吠える傾向・猫鳴きでない"),
Rule("cat", lambda f: (f["legs"] == 4) and (not f["has_wings"]) and (not f["habitat_water"]),
penalty=0.40, description="catなら4脚・翼なし・水生でないはず"),
Rule("cat", lambda f: f["meow"] and (not f["bark"]),
penalty=0.25, description="catならニャーで吠えない傾向"),
Rule("bird", lambda f: (f["legs"] in (2, 1)) and f["has_wings"],
penalty=0.40, description="birdなら翼があり脚は2本が多い"),
Rule("bird", lambda f: f["can_fly"] or f["has_wings"],
penalty=0.20, description="birdなら多くは飛べるか少なくとも翼あり"),
Rule("fish", lambda f: (f["legs"] == 0) and f["habitat_water"] and (not f["has_wings"]) and (not f["can_fly"]),
penalty=0.50, description="fishなら脚なし・水生・翼なし・飛ばない"),
]
rules_by_label = {}
for r in rules:
rules_by_label.setdefault(r.target_label, []).append(r)
def symbolic_penalty(label_str, x):
f = feature_dict(x)
penalty_sum = 0.0
violated = []
for r in rules_by_label.get(label_str, []):
ok = r.condition_fn(f)
if not ok:
penalty_sum += r.penalty
violated.append(r.description)
return penalty_sum, violated
# -----------------------------
# 4) 統合推論: ニューラル確率 - シンボリックペナルティ
# -----------------------------
def neuro_symbolic_predict(x, lambda_penalty=1.0, verbose=True):
"""
ニューラル確率 P(y|x) と symbolic ペナルティの重みつき差を最大化するラベルを選択。
P_adj(label) = P_nn(label) - lambda * penalty(label, x)
"""
x = x.reshape(1, -1)
probs = forward(x)[0] # (C,)
best_score = -1e9
best_label = None
evidence = {}
for idx, lab in enumerate(labels):
pen, vio = symbolic_penalty(lab, x[0])
score = probs[idx] - lambda_penalty * pen
evidence[lab] = {"p_nn": probs[idx], "penalty": pen, "score": score, "violations": vio}
if score > best_score:
best_score = score
best_label = lab
if verbose:
print("\n=== 統合推論レポート ===")
print("入力特徴:", feature_dict(x[0]))
for lab in labels:
e = evidence[lab]
print(f" [{lab}] P_nn={e['p_nn']:.3f} penalty={e['penalty']:.3f} score={e['score']:.3f}")
if e["violations"]:
for v in e["violations"]:
print(f" - ルール違反: {v}")
print(f">>> 最終予測: {best_label} (score={best_score:.3f})")
return best_label, evidence
# -----------------------------
# 5) テスト: いくつかの入力で挙動を確認
# -----------------------------
def sample_and_predict(legs, has_wings, can_fly, habitat_water, bark, meow, lambda_penalty=1.0):
x = np.array([legs, has_wings, can_fly, habitat_water, bark, meow], dtype=float)
return neuro_symbolic_predict(x, lambda_penalty=lambda_penalty, verbose=True)
# 例1: 0脚・水生 → fishが有力。ニューラルが誤る場合もルールで補正
print("\n### 例1: 0脚/水生/飛行なし")
sample_and_predict(legs=0, has_wings=0, can_fly=0, habitat_water=1, bark=0, meow=0)
# 例2: 4脚・吠える → dog寄りだが、もし水生=1なら dog ルール違反
print("\n### 例2: 4脚/吠える/水生=1 (dogっぽいが水生)")
sample_and_predict(legs=4, has_wings=0, can_fly=0, habitat_water=1, bark=1, meow=0)
# 例3: 4脚・ニャー → catが有力。ただし吠えるも1にするとルールが衝突
print("\n### 例3: 4脚/ニャー/吠える=1 (catっぽさとdogっぽさの衝突)")
sample_and_predict(legs=4, has_wings=0, can_fly=0, habitat_water=0, bark=1, meow=1, lambda_penalty=0.8)
参考文献
[R1] https://www.jstor.org/stable/40390679[R2] https://philpapers.org/rec/SHAFSA
[R3] https://www.academia.edu/716064/An_overview_of_strategies_for_neurosymbolic_integration
[R4] https://academic.oup.com/nsr/article/9/6/nwac035/6542460
[R5] https://dblp.org/rec/books/daglib/0007534.html
[R6] https://www.academia.edu/125564630/Markov_logic_networks
[R7] https://academic.oup.com/nsr/article/9/6/nwac035/6542460
[R8] https://link.springer.com/article/10.1007/s10462-023-10448-w
[R9] https://www.turingpost.com/p/neurosymbolic
[R10] https://files01.core.ac.uk/download/pdf/76361747.pdf
[R11] https://www.academia.edu/716064/An_overview_of_strategies_for_neurosymbolic_integration
[R12] https://ci.nii.ac.jp/ncid/BA60373564
[R13] https://homes.cs.washington.edu/~pedrod/papers/mlj05.pdf
[R14] https://arxiv.org/abs/1606.04422
[R15] https://arxiv.org/abs/2012.05876
[R16] https://academic.oup.com/nsr/article/9/6/nwac035/6542460
当サイトの内容、テキスト、画像等の転載・転記・使用する場合は問い合わせよりご連絡下さい。
エンジニアによるコラムやIDグループからのお知らせなどを
メルマガでお届けしています。




